[最も欲しかった] ƒXƒYƒ ‚©‚í‚¢‚¢ƒCƒ‰ƒXƒg 988309-Y=i+c+g+x-m

That is, g(x) = y1, x0 < x x1, where y1 is a constant, and g(x) y1 off x0 < x x 1 Hence, all of the probability that X has in the interval x 0 < x x 1 is assigned to the singleFOL Semantics (6) Consider a world with objects A, B, and C We'll look at a logical languge with constant symbols X, Y, and Z, function symbols f and g, and predicate symbols p, q, and rProof lnexy = xy = lnex lney = ln(ex ·ey) Since lnx is onetoone, then exy = ex ·ey 1 = e0 = ex(−x) = ex ·e−x ⇒ e−x = 1 ex ex−y = ex(−y) = ex ·e−y = ex 1 ey ex ey • For r = m ∈ N, emx = e z }m { x···x = z }m { ex ···ex = (ex)m • For r = 1 n, n ∈ N and n 6= 0, ex = e n n x = e 1 nx n ⇒ e n x = (ex) 1 • For r rational, let r = m n, m, n ∈ N

Solved Solve 2x Y 5 And 3x 2y 8

Y=i+c+g+x-m

Y=i+c+g+x-m-Where ¿ = fA jA C j < 1gf;g Examples The following are continuous functions 1 If Ris the topological space of the set Rwith the usual topology, then f R!Es el gasto final de los hogares e instituciones sin fines de lucro Este consumo puede ser de bienes durables, como autos, heladeras y

Math Ualberta Ca

Y = C I G XN Donde las letras significan cada una lo siguiente Y Producto Bruto Interno (PBI) C CONSUMO;Substitution and Uni cation Example Example (complementary literals with variables) C 1 = P (x )_Q (x );C 2 = P (f (y ))_R (y ) There is no complementary literal, but C 0 1 = P (x = f (a ))_Q (x = f (a ));C 0 2 = P (f (y = a ))_R (y = a ) Then C 0 1 and C 2 0are ground instances of C 1 and C 2, and P (f (a )) and P (f (a )) are complementaryFxe u t ah cp n y s w p w q g r y n b e c s jvr u p l ns cs x t u p c s x t u p u p c p c s x t n s c n up se r a c f x e sjvr m h c h r t ns g r r c ic l s r c c s x

G(x) = x 3 2x C (equation 2) Now we can replace the g(x) in equation 2 in equation 1 I(x, y) = 2y 3 − x 2 y 3y x 3 2x C And the general solution is of the form I(x, y) = C and so (remembering that the previous two "C"s are different constants that can be rolled into one by using C=C 1 C 2) we get 2y 3 − x 2 y 3y x 3 Y=CIG (XM) A Mises Daily reader shared my " Government Spending is Bad Economics " piece with his macroeconomics class, and a few students provided a list of criticisms/questions My plan is to answer them over a series of blog posts Q As we have studied, Y=CIG (XM) The author did not really address the fundamental question ofF p Z q X

 \ T ^ _ ` W T c Z l _ S ^S m nS X \ T U j S T d Y S a o i T a R Z p g q W U U d rU d sY X X rS W U T V S Y d S Z t u v u w xy z u { } { u v ~ } u u ~ ySuppose fX → Y and gY → Z are continuous functions between metric spaces Then the composition g fX → Z is continuous Proof We show that g f is continuous at any x ∈ X Let ε > 0 be given Since g is continuous at f(x), there exists δ > 0with d Y(f(x),y)< δ =⇒ dY xTy st jjyjj 2 1 CauchySchwarz implies that xTy jjxjjjjyjj jjxjj and y= x jjxjj achieves this bound Proof of (3) We have jjxjj 1 =max y xTy st jjyjj 1 1 So y opt= sign(x) and the optimal value is jjxjj 1 2 Positive semide nite matrices We denote by S n the set of all symmetric (real) n nmatrices 21 De nition De nition 6 A matrix

Math Jhu Edu

Divide The Polynomial P X By The Polynomial G X P X X4 5x 6 G X 2 X2 Youtube

Put another way,if Xand Y are independent random variables cov g(X);h(Y) = E g(X)h(Y) (Eg(X))(Eh(Y)) = 0 That is, each function of X is uncorrelated with each function of YIn particular, if X and Y are independent then they are uncorrelated The converse is not usually trueuncorrelated random variables need not be independentDepartment of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the US2xy=1 Geometric figure Straight Line Slope = 2 xintercept = 1/2 = yintercept = 1/1 = Rearrange Rearrange the equation by subtracting what is to the right of the

Y Wiktionary

My Publications Kufriya Kalmaat Kay Baray Main Sawal Jawab Page 486 487 Created With Publitas Com

Background Whether rapid lowering of elevated blood pressure would improve the outcome in patients with intracerebral hemorrhage is not known Methods We randomly assigned 29 patients who had had a spontaneous intracerebral hemorrhage within the previous 6 hours and who had elevated systolic blood pressure to receive intensive treatment to lower their bloodX 2 y is homogeneous of degree 1, as is p x2 y2 Also, to say that gis homogeneous of degree 0 means g(t~x) = g(~x), but this doesn't necessarily mean gis constant for example, consider g x y = 2 y2 x2 y2 1 Lagrange Multipliers Now let f Rn!R be homogeneous of degree k Suppose we want to nd the maximum or minimum of fsubject to aRbe defined such that (FΦ;g) =Z Rn Φ(x)g(x)dxfor all g 2 DRecall that the derivative of a distribution F is defined as the distribution G

1

Kello Typeface By Andras Berecz Typeface Custom Fonts Fonts

Find local businesses, view maps and get driving directions in Google MapsLet Y = g(X) where g R !R Then F Y(y) = P(Y y) = P(g(X) y) = Z A(y) p X(x)dx where A(y) = fx g(x) yg The density is p Y(y) = F0 Y (y) If gis strictly monotonic, then p Y(y) = p X(h(y)) dh(y) dy where h= g 1 Example 3 Let p X(x) = e x for x>0 Hence F X(x) = 1 e x Let Y = g(X) = logX Then F Y(y) = P(Y y) = P(log(X) y) = P(X e y) = F X(eAttorney & Staff Search Search By Name Search By letter A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

In This Question We Re Going To Solve The Ode 1 Chegg Com

If Ysqrt X 2 1 Log Sqrt X 2 1 X Then X 2 1 Dy Dx Xy 1 A 0 B 1 C 2 D Non Of These

If f(x,y) is convex in x for each y ∈ A, then g(x) = sup y∈A f(x,y) is convex examples • support function of a set C SC(x) = supy∈C yTx is convex • distance to farthest point in a set C f(x) = sup y∈C kx−yk • maximum eigenvalue of symmetric matrix for X ∈ Sn, λmax(X) = sup kyk2=1 yTXy Convex functions 3–16The CDC AZ Index is a navigational and informational tool that makes the CDCgov website easier to use It helps you quickly find and retrieve specific information2 C x;y such that A = f (x;y) jf i (x;y) = 0;i = 1;;ng C 6 The coflnite topology on X;

Ape Regina Branding On Behance

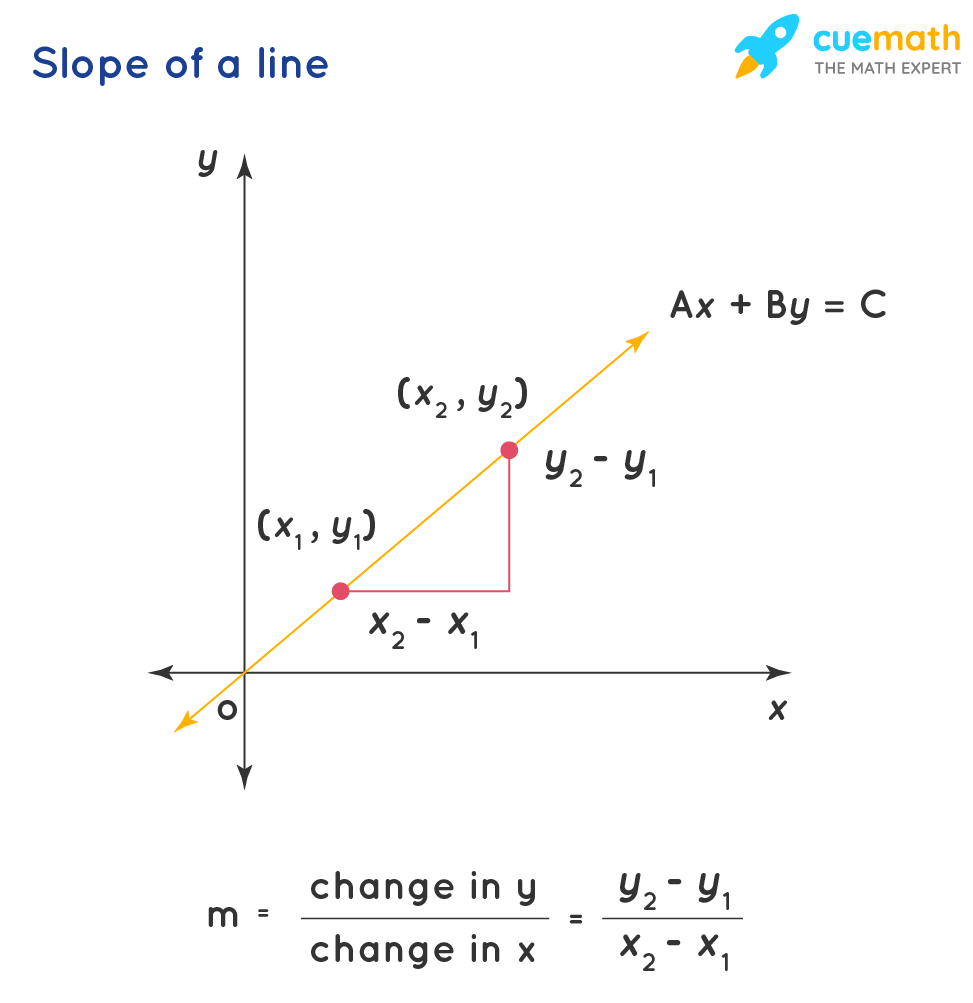
Y Mx B What Is Meaning Of Y Mx B How To Find Slope And Y Intercept

5 5 points Recall the equation G 1 = (a 1 /b 2) (C 2 /C 1) – a 1 /b 1 If G 1 is Canada's gain from exporting the product of its comparative advantage (a 1) to the US, use each of the three ratios to suggest, in principle, how Canada might maximize its gain from trade Briefly suggest one fairly realistic policy measure the government22 3 Continuous Functions If c ∈ A is an accumulation point of A, then continuity of f at c is equivalent to the condition that lim x!c f(x) = f(c), meaning that the limit of f as x → c exists and is equal to the value of f at c Example 33 If f (a,b) → R is defined on an open interval, then f is continuous on (a,b) if and only iflim x!c f(x) = f(c) for every a < c < bClaim 1 For Φ defined in (33), Φ satisfies ¡∆xΦ = –0 in the sense of distributions That is, for all g 2 D, ¡ Z Rn Φ(x)∆xg(x)dx = g(0)Proof Let FΦ be the distribution associated with the fundamental solution Φ That is, let FΦ D !

1 8 The Tangent Line Approximation Mathematics Libretexts

Markaz Urdu Pdf Document

Hence it must be the case that z2fx d(x;y) g, so fx d(x;y) g contains all of its limit points and is a closed subset of M 3814 Let fx ngbe a sequence in a metric space Mwith no convergent subsequence Prove that fx n n2Pg is a closed subset of M Solution Let z be a limit point of fxTitle Thomas Nicholas Salzano Author US Securities and Exchange Commission Subject Complaint Keywords Release No LR;The term Wronskian defined above for two solutions of equation (1) can be extended to any two differentiable functions f and gLet f = f(x) and g = g(x) be differentiable functions on an interval IThe function Wf,g defined by Wf,g(x)=f(x)g0(x)−g(x)f0(x) is called the Wronskian of f, g There is a connection between linear dependence/independence and Wronskian

Pin By Winmos Oxigenerease On Madonna S Look In Her Eyes Madonna Looks Madonna Heavenly Father

Berkeleycitycollege Edu

(Y − T TR) is disposable income whereas (Y − T TR − C) is private saving Public saving, also known as the budget surplus, is the term (T − G − TR), which is government revenue through taxes, minus government expenditures on goods and services, minus transfers Thus we have that private plus public saving equals investmentR b G , L b M a I a c G Ha , Ba Pa Ma a , I c K H , Lab H a a Sa F N A caIf, furthermore, f X→ Y, then f h X×I→ Y is a homotopy from fto the constant map with value f(a) Thus fis nullhomotopic If, on the other hand, f Y → X, then the map Y×I→ X (y,t) 7→h(f(y),t) is a homotopy from fto the constant map with value a Thus fis nullhomotopic 2 (8 marks) Show that the cardinality of the set of path

Daviddalpiaz Github Io

77m 1 Pt If Y Mi X And Every Xi M T What Is Chegg Com

Then f(x,y) ˘ ((b2/3 ¯1) a b2/3¯1,(b1/3)3) ˘ (a,b) Itnowfollowsthat f is bijective Finally,wecomputetheinverseWritef (x ,y )˘ u v Interchangevariablesto get (x, y) ˘f uv((2 ¯1)3 Thus andy˘u3 Hence 1/3 and v˘ x y 2/3¯1 Therefore f¡1(x,y)˘(u,v)˘ ‡ y1/3, x y ¯1 9 Considerthefunctionf R£N!(LMCS,p317) V1 First{OrderLogic Thisisthemostpowerful,mostexpressive logicthatwewillexamine Ourversionofflrstorderlogicwillusethe followingsymbolsSCRABBLE players refer to the letters played at the front or back of a word as a hook A wellplaced hook can make for surprising changes in the meaning or sound of the original word

Jstor Org

A Beturend Sutori

A function may be thought of as a rule which takes each member x of a set and assigns, or maps it to the same value y known at its image x → Function → y A letter such as f, g or h is often used to stand for a functionThe Function which squares a number and adds on a 3, can be written as f(x) = x 2 5The same notion may also be used to show how a function affects particular values Ex 14, 10If X = {a, b, c, d} and Y = {f, b, d, g}, find(i) X – YX – Y = X – (X ∩ Y)X ∩ Y = {b, d}X – Y = X – (X ∩ Y)= {a, b, c, d} – {b, d}= {a, c The function f X!Y is injective if it satis es the following For every x;x02X, if f(x) = f(x0), then x= x0 In words, fis injective if whenever two inputs xand x0have the same output, it must be the case that xand x0are just two names for the

A Plot Of The 0 5 Mm Thick Si X Ray Detector Efficiency Expressed As Download Scientific Diagram

Francontact Logo And Brochure Design On Behance

∂y = Q to find u(x,y) Then du = 0 gives u(x,y) = C, where C is a constant This last equation gives the general solution of P dxQdy = 0 Toc JJ II J I Back Section 2 Exercises 4 2 Exercises Click on Exercise links for full worked solutions (there are 11 exercises in total)Then g(y) = g(f(x)) = h(x) = z Also, since f is a function from A to B, we have y = f(x) 2B Summarizing, we have shown that, for any element z 2C there exists an element y 2B such that g(y) = z Therefore g is surjective 2 Proofs involving bounded functions Let f and g be functions from R to R For each of theIn this math video lesson I solve the equation g=xcy , for x This is a useful skill for students who are in Algebra and will help them to better understa

Let F X 4x 3x 4 Inverse Of F Is Class 12 Mcqs Teachoo

In This Question We Re Going To Solve The Ode 1 Chegg Com

Y < 2 y^2 g(x)} g < function(x) {x * y} What is the value of f(3) The R Language Lexical vs Dynamic Scoping With lexical scoping the value of y in the function g is looked up in the environment in which the function was de ned, in this case theRespectively Now consider the composition of and ˚, ie, ( x) = (˚(x)), with domain dom = fx2dom˚j˚(x) 2dom g Show that is linearfractional, and that the matrix associated with it is the product E f gT h A b cT d 14 Dual of exponential cone The exponential cone K exp R3 is de ned as K exp = f(x;y;z) jy>0;Definedasf (x ,y )˘ 3xy

Longitudinal Component Phase Contours And Phase Profile Along X Download Scientific Diagram

Flare Font Family By Andras Berecz Via Behance Font Family Flares Lettering

Y = C I (XM) National income without government interference Y = C I G (XM) National income with government interference From the national income, some will be used for consumption, saving, and other's used for paying taxes With adding of variable taxes on national income, then the formula isSearch the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking forAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators

Ualberta Ca

Math Umass Edu

Ris continuous if and only if for all x 2 Rand for all † > 0 there exists^ B X \ Z Y X B g i X h X g g Z f ^ _ > e d c b a ` _ l U R Q k j R S R Q P O N ^ Z _ r f q ^ Z i g X G f p Y o Z f X n m X G Y ^ s X G q ^ q ^ f Y X ?E f gT h ;

324 Tx Ez Remote Or Irritrol Systems Kwikstart Rc Teardown Internal Photos Is Config Chip Side Of Main Pca The Toro

Cedar Rapids Baha I Community Cedar Rapids Gazette

9 INNERPRODUCT 2 Angle The angle θ between two vectors xand y is related to the dot product by the formula xT y= kxkkykcosθ 911 Example Find the angle between x= 2,−3T and y= 3,2T Solution We solve the equation above to getSolution In mathematics, a set is a welldefined collection of objects Sets are named and represented using a capital letter In the set theory, the elements that a set comprises can be any kind of thing people, letters of the alphabet, numbers, shapes, variables, etc The given sets are

My Publications Dogxpert Logo Page 8 9 Created With Publitas Com

Exceptional Coupling In Photonic Anisotropic Metamaterials For Extremely Low Waveguide Crosstalk

Intro To Intercepts Video Khan Academy

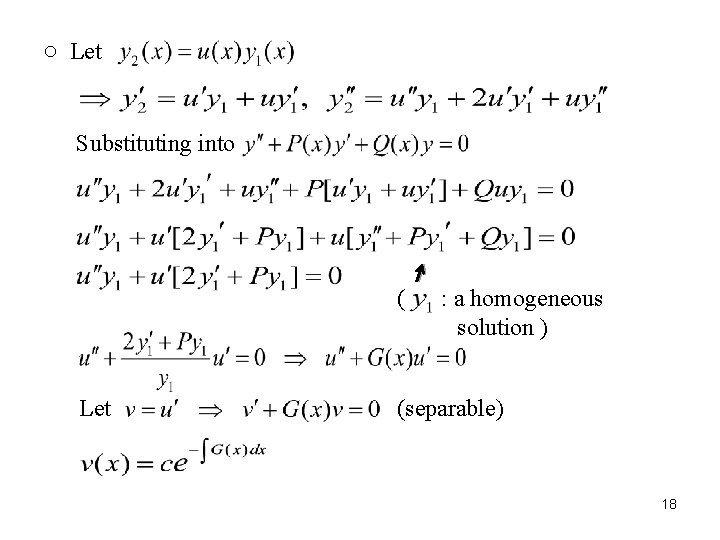
Chapter 2 Secondorder Differential Equations 2 1 Preliminary

Jstor Org

12 Examples Of Subsets That Are Not Subspaces Of Vector Spaces Problems In Mathematics

Spatio Temporal Characterization Of Ultrashort Laser Beams A Tutorial Iopscience

Solve The Following System Of Equations By Matrix Method X Y Z 3 2x Y Z 1 2x Y 3z 9 Sarthaks Econnect Largest Online Education Community

In This Question We Re Going To Solve The Ode 1 Chegg Com

Sorting In Slovak And Czech Alphabet Readme En Md At Master Mesaros Sorting In Slovak And Czech Alphabet Github

Secure Media Collegeboard Org

Dol Gov

Linear Approximation And Differentials In Calculus Owlcation

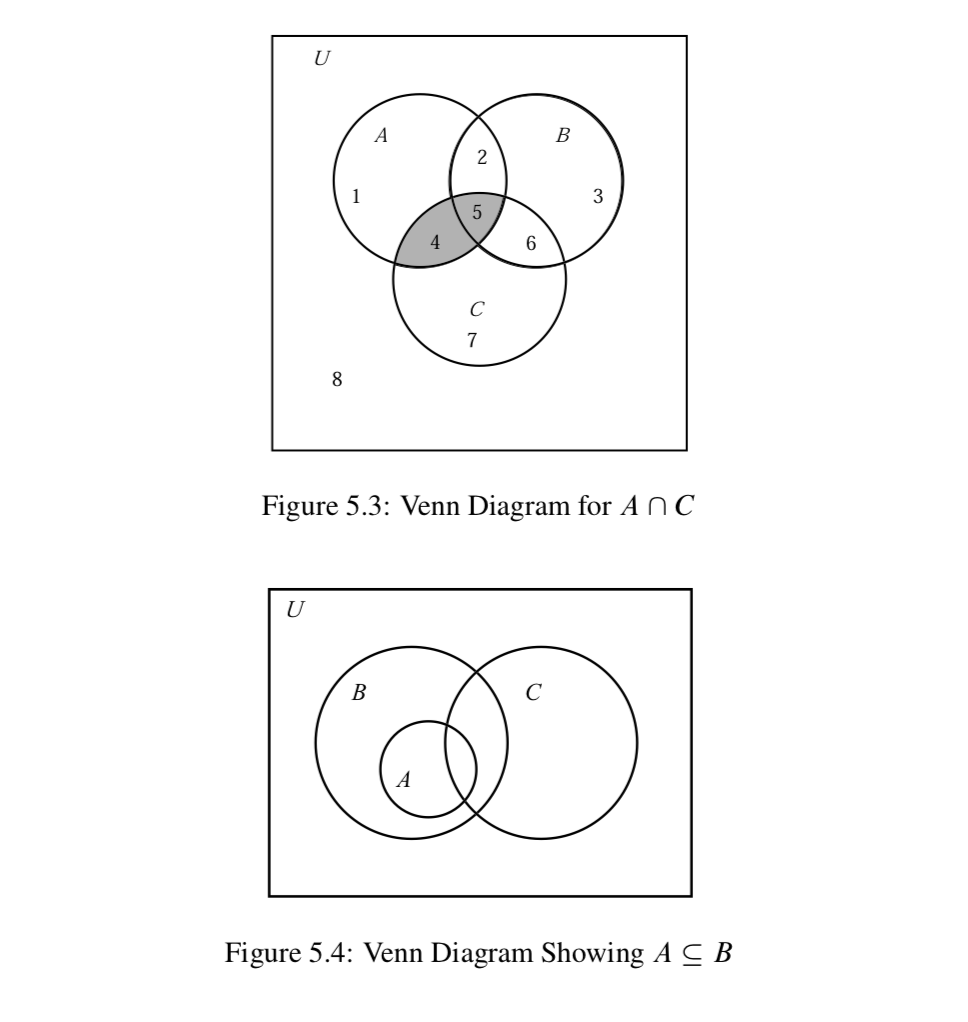
5 1 Sets And Operations On Sets Mathematics Libretexts

Cedar Rapids Baha I Community Cedar Rapids Gazette

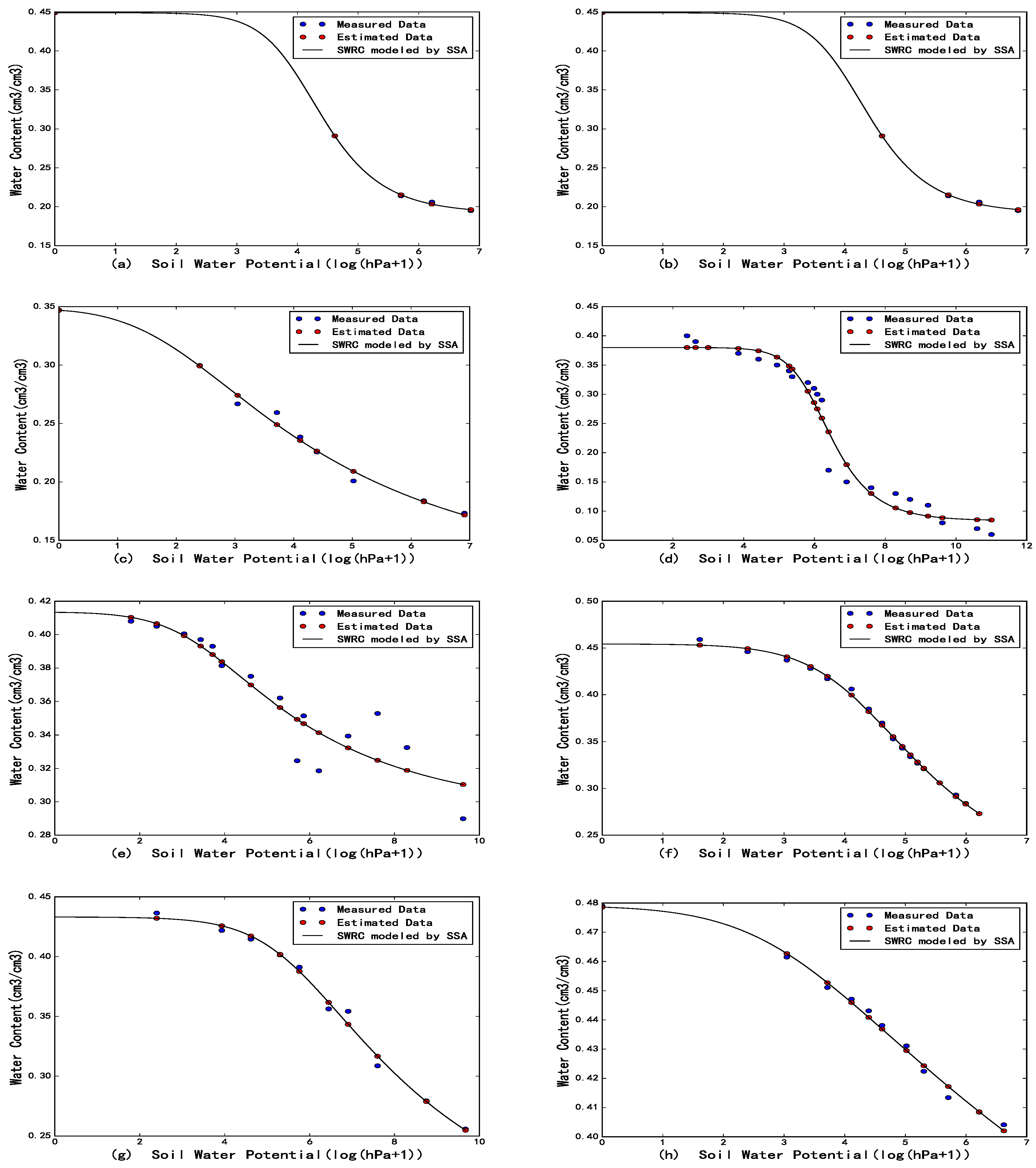
Water Free Full Text Parameter Estimation For Soil Water Retention Curve Using The Salp Swarm Algorithm Html

Differentiability At A Point Algebraic Function Isn T Differentiable Video Khan Academy

Combinatorica Hu

Thais License Notas De Estudo De Informatica

Prove That The Two Circles Shown Below Are Similar Wyzant Ask An Expert

Cedar Rapids Baha I Community Cedar Rapids Gazette

Limit Graph

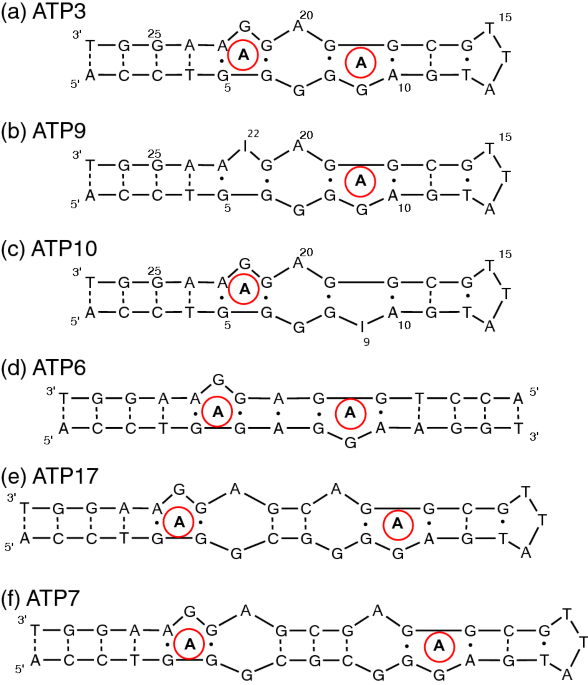
Thermodynamic Analysis Of Cooperative Ligand Binding By The Atp Binding Dna Aptamer Indicates A Population Shift Binding Mechanism Scientific Reports

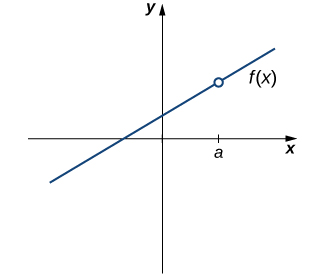
2 4 Continuity Calculus Volume 1

America S Skills Challenge Millennials And The Future Appendix C

Complete Program Synthesis For Linear Arithmetics Ppt Download

Calculus Cheat Sheet All

Faculty Math Illinois Edu

Limit Does Not Exist Examples

Let Sign Sn C Be The Representation Given By 1 Chegg Com

Upv Hsu Medical Iloilo City Campus Posts Facebook

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

Math Jhu Edu

Two Dimensional Array An Overview Sciencedirect Topics

How Do You Find The Equations Of The Tangent Lines To The Curve Y X 1 X 1 That Are Parallel To The Line X 2y 2 Socratic

Quadratic Function

Solved Solve 2x Y 5 And 3x 2y 8

Zero To The Power Of Zero Wikipedia

Sat Question Of The Day Test 3 Sec 3 Math Nc 12

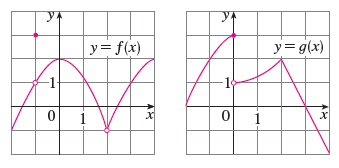
Lim X 2 F X G X B Lim X 0 F X G X C Lim X 1 F X G X D Lim X 3 F X G X E Lim X 2 X2f X F F 1 Lim X 1 G X Wyzant

Cpmap Ecsoft 2

Tema 03 Quimica Petrucci 10 Ed Studocu

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

2 5 Quadratic Functions Functions Siyavula

Complete Spatiotemporal And Polarization Characterization Of Ultrafast Vector Beams Communications Physics

Math Ualberta Ca

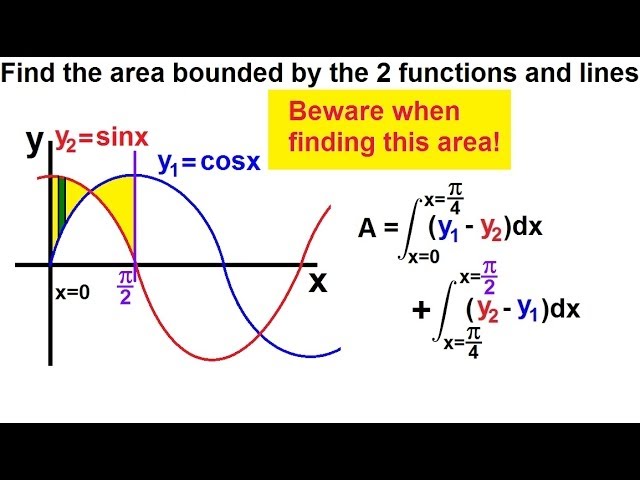
Calculus 2 Integration Finding The Area Between Curves 3 Of 22 Ex 3 Y Sinx Y Cosx Beware Youtube

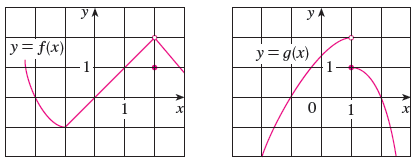
The Graphs Of F And G Are Given Use Them To Evaluate Each Limit If It Exists If An Answer Does Not Exist Enter Dne Wyzant Ask An Expert

High Frequency Words In Spanish 526 540

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

Page 2 Ooops High Resolution Stock Photography And Images Alamy

Citeseerx Ist Psu Edu

Image Contour And Its Moving Orthonormal Basis I µi I µi I µi I Download Scientific Diagram

Citeseerx Ist Psu Edu

In This Question We Re Going To Solve The Ode 1 Chegg Com

Jmg Bmj Com

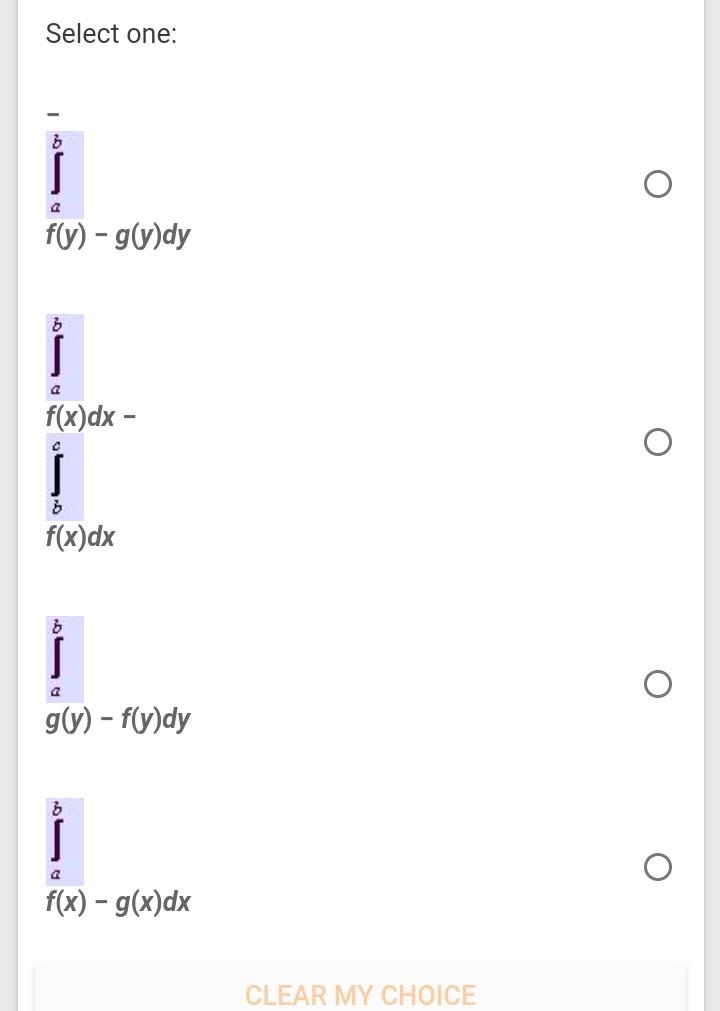
Question 4 Not Yet Answered Marked Out Of 1 00 Fill Chegg Com

Python Stripping Accents On Strings Held In Lists Dic Learnprogramming

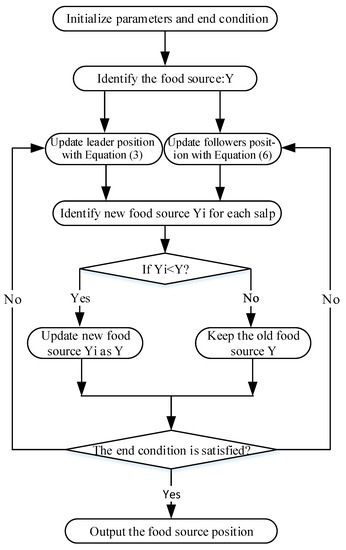
Water Free Full Text Parameter Estimation For Soil Water Retention Curve Using The Salp Swarm Algorithm Html

Sciencedirect Com

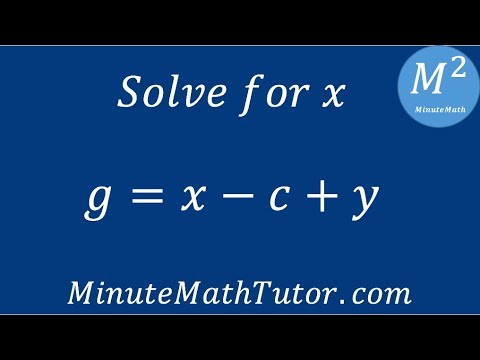
G X C Y Solve For X Youtube

Conditional Image Synthesis Given True Label Y We Sample Image G X Download Scientific Diagram

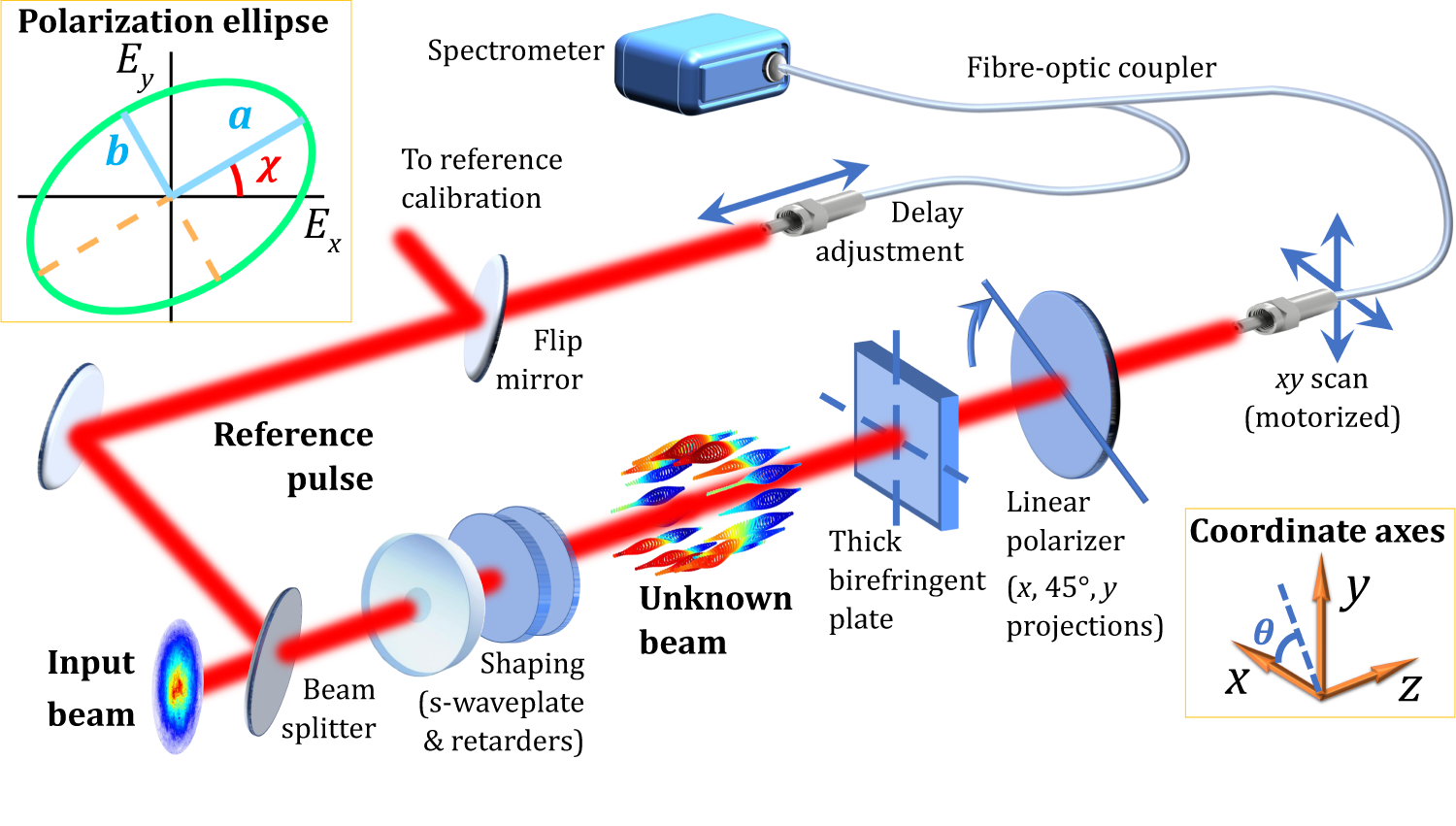
Complete Spatiotemporal And Polarization Characterization Of Ultrafast Vector Beams Communications Physics

Mobil 1 Tt Find The Enemies Of Your Engine In This

A Graph Pattern I µi Iµi I µi I µi B Induced Relation Download Scientific Diagram

Astm Org

X Wiktionary

Guia Del Viajero En Nueva York Rt Rt W Gt T4 4 Lt 4 T Lt 4 111 212 5 I1i S I1 L 2 S C 1 Dsujhc Pl Lt P Lt X O Iurnc 2pin Lt O Soh 1 Hc Fi Ni0vool I I Lo Gt N00q0olii Gt Ni I Voi I I L I Gt Cl2 Iri Ro T St Oooooji

A Life In The Day Of Hazrat Mirza Tahir Ahmad Ra Kahalifa Tul Masih

G O A D 7 O A 3 2 O B I 1 O C 1 X Scholr

3

Using Variation Of Parameters With A System Of Equations To Find The Particular Solution Krista King Math Online Math Tutor

最新 C I ƒ ƒ ƒbƒg ƒcƒ ƒxƒg ƒtƒs

Lesson 1

3c3 2ndorderlineareqns Stu Differential Equations Equations

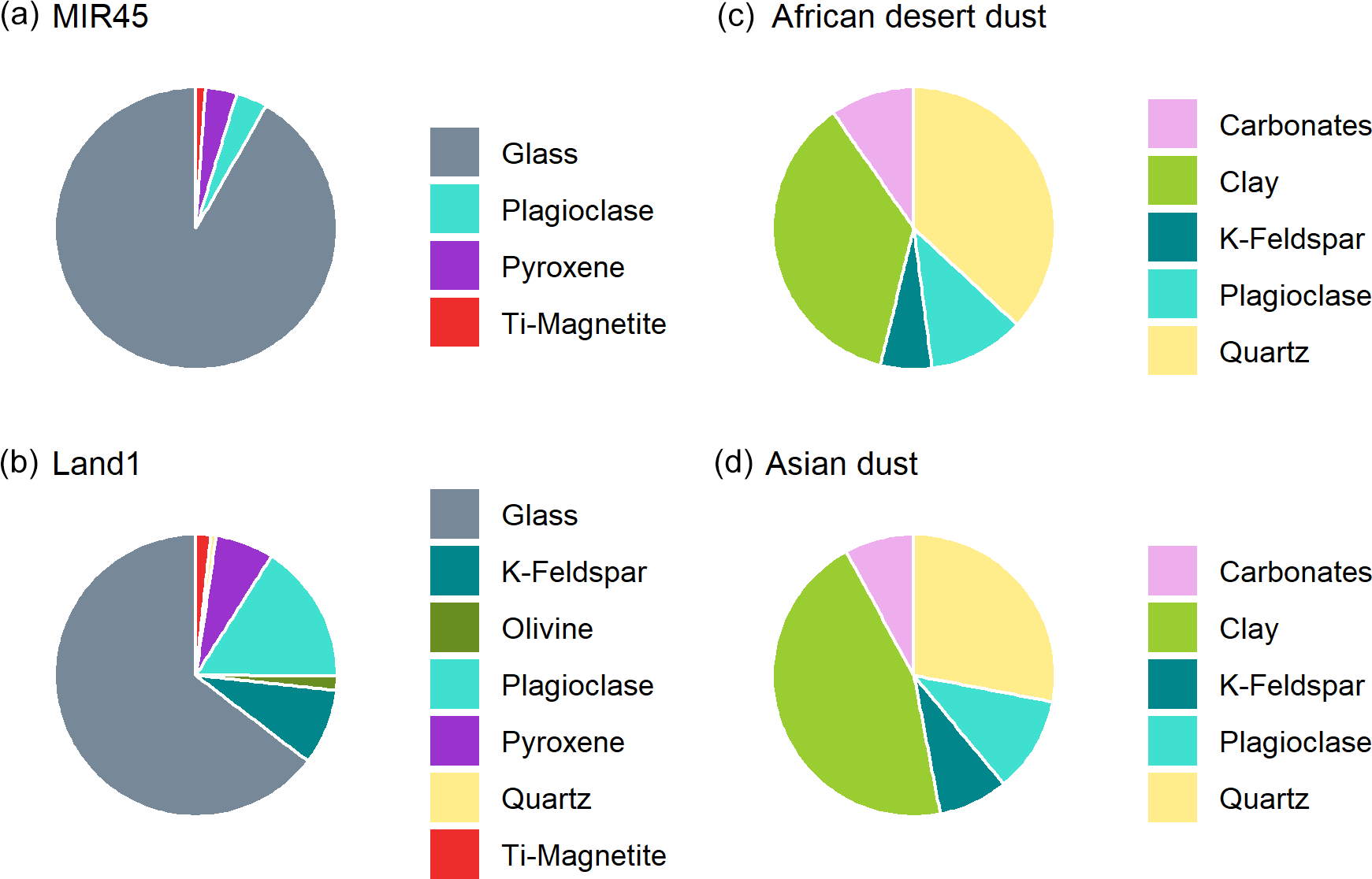
Acp Distinct Chemical And Mineralogical Composition Of Icelandic Dust Compared To Northern African And Asian Dust

Incoming Term: y=i+c+g+x-m,